初中几何模型 - 非平行 A 字型相似操作说明
一、操作指南
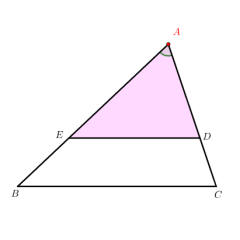
复位布局点击 “复位” 按钮,可将模型恢复至初始状态:呈现△ABC 及△AED 的基础图形,重置所有滑块与按钮的默认状态。
E 点位置调整拖动 “E 点位置” 滑块,可改变 E 在 AB 上的位置,同步观察△AED 的形态变化,直观感知相似比、线段乘积及面积比的动态变化。
图形变换演示
拖动 “△AED 翻折” 滑块,演示△AED 翻折后的形态,体现非平行 A 字型的变换过程;
拖动 “△AED 旋转” 滑块,演示△AED 旋转后的形态,展示模型的变换逻辑;
点击 “翻折 - 旋转” 按钮,一键演示△AED 翻折 + 旋转的组合变换过程,呈现非平行 A 字型的形成逻辑。
二、用途说明与应用场景(一)学生端(针对 “非平行 A 字型相似的核心认知” 场景)
明确核心条件:掌握该模型的触发条件是 “∠AED=∠ACB”(共角 + 一组角相等);
掌握核心结论:熟练应用相似后的线段乘积关系(AE・AB=AD・AC),理解相似三角形的面积比为相似比的平方;
认知特殊规律:明确 “△AED 与△ABC 的面积比 = AE・AD/(AB・AC)” 这一结论,即使两三角形不相似也成立。
(二)教师端(针对 “非平行 A 字型相似的深化教学” 场景)
动态展示变换:通过滑块与按钮演示翻折、旋转过程,帮助学生理解非平行 A 字型的形成逻辑;
分层适配教学:基础层聚焦 “∠AED=∠ACB→△AED~△ACB” 的相似识别,进阶层聚焦 “线段乘积、面积比的推导与特殊规律”;
关联模型体系:将非平行 A 字型与平行 A 字型对比,完善 A 字型相似的完整认知框架。
三、教学应用案例
情境导入(4 分钟)展示初始模型,提出问题:“当∠AED=∠ACB 时,△AED 与△ACB 有什么关系?它们的线段、面积会呈现怎样的规律?”
操作演示(8 分钟)
点击 “复位”,引导学生识别核心条件 “∠AED=∠ACB”;
拖动 “E 点位置” 滑块,暂停提问:“E 点移动时,相似比与面积比的变化有什么规律?”;
点击 “翻折 - 旋转” 按钮,演示变换过程,暂停提问:“非平行 A 字型是通过什么变换形成的?”;
说明面积比的特殊规律,提问:“两三角形不相似时,面积比的结论还成立吗?”
互动任务(3 分钟)
基础层任务:描述非平行 A 字型相似的核心条件与相似结论;
进阶层任务:推导 “AE・AB=AD・AC” 的依据,并说明面积比特殊规律的适用场景。
总结(2 分钟)梳理核心逻辑:“非平行 A 字型相似的核心条件是‘共角 + 一组角相等’,结论包含相似关系、线段乘积及面积比;其中面积比的特定公式即使不相似也成立,是 A 字型相似中区别于平行 A 字型的特殊模型。”
 浏览量:545
浏览量:545