考生网初中几何模型 - 垂线段最短模型典例 1
一、操作指南(适配考生网交互式几何学习场景)
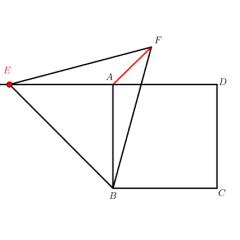
- 初始化点击 “初始化” 按钮后,包含△ABC(AB=4、∠BAC=45°)、∠BAC 的角平分线 AD、动点 E(AD 上)、F(AB 上)的图形会恢复至典例初始布局,确保探究起点一致,适配课堂演示与自主学习流程。
- 全显示点击 “全显示” 按钮后,会一次性呈现该典例的核心逻辑 —— 三角形角平分线背景下 BE+EF 最小值的判定依据,将 “三角形角平分线 + 双动点 + 垂线段最短” 的复合逻辑转化为可视化步骤,降低抽象几何题的理解难度。
- 上一步 / 下一步
- 点击 “下一步”:逐步呈现 E 点沿 AD、F 点沿 AB 运动时 BE+EF 的变化逻辑、最值状态的形成原理,拆分中考三角形角平分线背景下线段和最值难题的解题步骤,帮助学生掌握核心解法;
- 点击 “上一步”:回退至前一画面,便于学生自查错误、教师课堂复盘细节。
- 动态演示 / 暂停动画
- 点击 “动态演示”:自动演示 E 点沿 AD、F 点沿 AB 运动的过程,同步呈现 BE+EF 的数值变化,让双动点与线段和的关联更直观,帮助学生理解三角形角平分线下的最值规律;
- 点击 “暂停动画”:锁定 E、F 的运动状态,方便聚焦 BE+EF 取最小值的时刻,适配学生自主观察与教师讲解需求。
- 最小值按钮点击后自动定位 BE+EF 取最小值时的 E、F 点状态,同步展示对应的几何依据(角平分线的对称性质 + 垂线段最短逻辑),帮助学生快速掌握三角形角平分线背景下线段和最值题的核心解法。
- 动态验证复选框勾选后会显示 BE、EF 及 BE+EF 的实时数值,通过数值对比强化对 “BE+EF 最小值对应垂线段位置” 的理解,让抽象结论更具说服力。
- 点拖动操作按照界面说明 “点 B、C、E、F 可拖动”,手动拖动任意点时,平台会实时同步图形与线段长度的变化,直观呈现 “点位置 - 线段和” 的联动规律,支持学生自主探索三角形角平分线下的垂线段最短逻辑。
- 窗口辅助操作
- 拖动图形区域可调整显示位置,避开遮挡以聚焦△ABC、角平分线 AD 及动点的构造细节;
- 调整窗口视角可更清晰观察 E、F 的运动轨迹与 BE+EF 的数值关联,辅助理解双动点的最值逻辑。
二、用途说明(含分层教学适配)
(1)对学生
精准突破中考综合考点
聚焦 “三角形角平分线 + 双动点 BE+EF 最小值” 这一中考几何高频难点,通过交互功能自主梳理 “角平分线构造 - 双动点运动 - 垂线段最短” 的解题逻辑,攻克几何综合题的丢分点。
学习更直观高效
借助动态演示与数值同步功能,摆脱被动记忆,将 “三角形角平分线 + 双动点 + 线段和最值” 的抽象原理转化为可视可操作的过程,降低学习难度,提升理解深度与学习效率。
构建系统化知识体系
结合考生网 “垂线段最短系列”“三角形几何系列” 模型,联动训练不同场景的动点最值题,构建覆盖中考几何核心题型的知识框架。
(2)对教师
轻松演示复杂题型
无需手绘三角形、角平分线、双动点等图形,通过 “动态演示 + 全显示” 功能快速展示 BE+EF 的变化规律,5 分钟即可讲透原本需大量板书的三角形角平分线最值逻辑,节省课堂时间。
分层教学适配全层次学生
基础层学生:通过 “全显示 + 最小值” 按钮聚焦结论与构造步骤,配套 “跟着操作标记动点” 的任务,帮助后进生跟上课堂节奏;
进阶层学生:引导自主拖动 B、C 点,观察不同三角形布局下的线段和变化,总结角平分线背景下的垂线段最短核心规律;
拔高层学生:布置 “自主设计三角形角平分线 + 三动点线段和最值” 变式题,借助模型验证思路,提升尖子生的几何创新解题能力。
丰富教案内容
预设的交互步骤可直接整合至教案,让几何课从 “枯燥讲题” 转变为 “互动探究”,活跃课堂氛围,提升教学质量。
三、教学应用案例与实施策略
(1)课堂教学案例:八年级 “三角形角平分线 + 双动点最值” 探究课(20 分钟片段)
- 情境导入展示 “△ABC 中,AD 是角平分线,需在 AD、AB 上分别找一点 E、F,使 BE 到 F 的路径最短” 的几何情境,提问 “E、F 应在何处时,BE+EF 最短?”,引出本模型。
- 模型操作
- 点击 “动态演示” 按钮,演示 E 沿 AD、F 沿 AB 运动的过程,引导学生观察 BE+EF 长度的变化趋势;
- 点击 “最小值” 按钮,定位 BE+EF 取最小值时的 E、F 状态,引导学生观察此时的角平分线对称构造与垂线段关联。
- 分层任务
- 基础层:跟着操作标记出 BE+EF 最小时的 E、F 位置,写出 “利用角平分线对称 + 作垂线段” 的解题步骤;
- 进阶层:拖动 B、C 点调整三角形布局,重复操作并记录 BE+EF 的变化规律,总结角平分线背景下的最值特征;
- 拔高层:尝试在 AC 上增加动点 G,设计 “BE+EF+FG” 的最值问题,借助模型验证构造思路。
- 总结反馈各层次学生分享结果,借助 “全显示” 功能梳理 “三角形角平分线 + 垂线段最短” 的核心逻辑,强化认知。
(2)分层教学实施策略
| 学生层次 | 教学任务设计 | 模型工具应用 |
|---|---|---|
| 基础层 | 1. 模仿操作标记 BE+EF 最小时的 E、F 位置;2. 背诵角平分线背景下垂线段最短的解题步骤 | 用 “全显示 + 最小值” 呈现结论,配套 “一步一操作” 指引 |
| 进阶层 | 1. 自主拖动 B、C 点,探索 BE+EF 的变化规律;2. 总结三角形角平分线背景下的垂线段最短核心规律 | 用 “点拖动 + 动态验证” 观察数值变化,总结构造共性 |
| 拔高层 | 1. 设计三角形角平分线 + 多动点的线段和最值变式题;2. 用模型验证构造思路并修正错误 | 用 “点拖动 + 三角形布局调整” 自主探究,借助动态演示验证猜想 |
(3)课后巩固分层任务
基础层:通过模型重复操作 2 次不同三角形布局的案例,记录 BE+EF 取最小值时的构造步骤;
进阶层:完成 2 道中考 “三角形角平分线 + 双动点线段和” 结合的最值真题,用模型验证答案的合理性;
拔高层:总结 3 种 “三角形背景下垂线段最短” 的构造方法,结合模型的数值功能佐证结论。
 浏览量:955
浏览量:955