初中几何模型 - 阿基米德折弦定理典例 2
一、操作指南(适配考生网交互式几何学习场景)
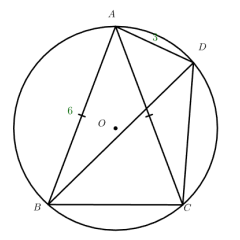
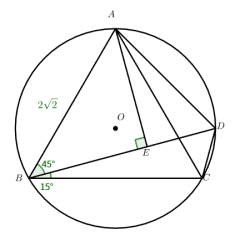
初始化点击 “初始化” 按钮后,包含内接于⊙O 的等腰 Rt△ABC、另一侧半圆上的点 D、DE⊥BC 的图形会恢复至典例初始布局,重置所有展示状态,确保探究起点一致。
全显示点击 “全显示” 按钮后,会一次性呈现 “等腰 Rt△ABC 的标注→AB+BE=CE 的折弦关系标注→DE⊥BC 的垂直关系标注” 的完整条件展示,明确典例的核心图形与关系条件。
步骤切换(上一步 / 下一步)点击 “下一步” 按钮,可逐步展示典例的辅助线添加流程(点击 “上一步” 可回退至前一操作状态):
操作步骤 1:展示 “连接 AD、CD(关联圆内接图形的线段关系)” 的辅助线添加效果;
操作步骤 2:展示 “构造适配折弦定理的线段(如关联 AB+BE=CE 的折弦关系)” 的辅助线添加效果;
操作步骤 3:展示 “聚焦等腰直角三角形与点 D 的角度关联” 的标注效果。
窗口内容拖动调整拖动图形区域内的⊙O、等腰 Rt△ABC、点 D、辅助线及相关标注,可自主调整其在界面中的显示位置,避免遮挡,更清晰地查看 “圆内接等腰直角三角形 + 折弦关系” 的复合图形关系。
全屏播放与退出点击界面中图形区域的 “全屏播放” 按钮:可将几何图形与操作流程切换至全屏模式,优化复合条件下图形关系的展示效果;退出全屏:在全屏模式下,按下键盘 “ESC” 键,即可恢复原界面布局。
二、用途说明(含分层教学适配)
(1)对学生
掌握圆内接等腰直角三角形场景的折弦定理辅助线策略通过分步展示的辅助线操作,明确 “圆内接等腰直角三角形中,优先关联折弦关系(AB+BE=CE)适配折弦定理” 的图形操作策略,攻克该场景下折弦定理应用的辅助线添加难点。
强化折弦关系的应用能力借助操作流程中条件与图形的关联标注,掌握 “圆内接等腰直角三角形 + DE⊥BC+AB+BE=CE” 与折弦定理的结合操作方式,提升定理在特殊三角形场景中的应用分析能力。
构建特殊三角形内接圆场景的折弦定理操作体系结合考生网 “初中几何模型” 系列内容,联动理解 “圆内接等腰直角三角形 + 折弦关系” 的题型特征,形成以辅助线操作为核心的特殊三角形场景分析框架。
(2)对教师
高效展示特殊三角形场景的图形操作逻辑无需手动分步绘制辅助线,通过 “上一步 / 下一步” 按钮快速呈现辅助线添加与条件关联流程,节省课堂中特殊三角形场景下折弦定理应用的演示时间。
分层教学适配全层次学生
基础层学生:通过步骤展示,配套 “标记等腰 Rt△ABC 与 DE⊥BC” 的任务,掌握基础图形操作步骤;
进阶层学生:结合步骤逻辑,梳理 “圆内接等腰直角三角形→折弦关系→折弦定理关联” 的几何关系链条,总结特殊三角形场景的操作规律。
丰富课堂互动形式以 “分步辅助线展示 + 折弦关系标注” 替代传统板书推导,让特殊三角形场景下折弦定理的探究更具直观性与条理性,提升学生课堂参与度。
三、教学应用案例与实施策略
(1)课堂教学案例:九年级 “阿基米德折弦定理的特殊三角形场景应用” 操作课(20 分钟片段)
情境导入展示初始布局的典例 2 图形,提问 “圆内接等腰直角三角形中存在折弦关系时,如何通过图形操作关联阿基米德折弦定理?”,引出本典例的操作演示;
模型操作
点击 “初始化”,恢复典例初始布局;
点击 “全显示”,完整呈现所有条件与关系标注;
点击 “下一步”,逐步展示辅助线添加流程,引导学生识别每一步对应的定理应用关联;
拖动图形区域内容,调整显示位置,清晰聚焦核心图形关系;
点击 “全屏播放”,在大屏模式下清晰展示完整操作流程;
分层任务
基础层:在展示界面中标记等腰 Rt△ABC 与 DE⊥BC,明确典例的基础图形条件;
进阶层:结合步骤逻辑,独立描述每一步辅助线操作的目的,自主梳理特殊三角形场景与折弦定理的关联逻辑;
总结反馈引导学生结合操作内容,总结 “特殊三角形内接圆场景下折弦定理应用的操作要点(核心:关联特殊三角形特征与折弦关系适配定理;辅助线:聚焦线段与角度的对应关系)”,强化对特殊三角形场景操作的认知。
 浏览量:363
浏览量:363