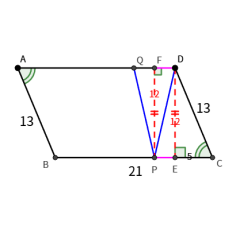
平移边或对角线，构造特殊四边形_动态模型演示

平移边或对角线，构造特殊四边形操作说明

操作指南：

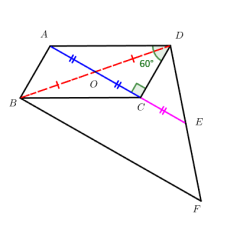
功能相关：初始化 / 全显示：展示□ABCD、BD（∠CDB=60°）、点 E（AB 上）、CE（CE=BD）的结构；上一步 / 下一步：逐步推进 “平移 CE 构造平行四边形→证明等边三角形→推导线段数量关系” 的过程，直观呈现 “平移边构特殊四边形” 的辅助线作用；
视图相关：拖动图形区域可调整展示位置；点击 “全屏播放” 切换全屏模式，适配沉浸式观察。

用途说明：

对学生：

掌握平行四边形中平移构造特殊图形的解题方法：通过步骤演示，分步学习核心逻辑：

作辅助线：过 D 作 DF∥CE，交 AB 的延长线于 F，利用 AB∥CD、DF∥CE，构造□DFCE；
平行四边形性质：由□DFCE 得 DF=CE，EF=CD（平行四边形对边相等）；
关联已知条件：由 CE=BD，得 DF=BD；
证等边三角形：□ABCD 中 AB∥CD，故∠ABD=∠CDB=60°，结合 DF=BD，得△BDF 是等边三角形，因此 BF=BD；
推导数量关系：BF=BE + EF，代入 EF=CD，得BE + CD = BD，解决 “平行四边形中线段数量关系证明无思路” 的问题。

对教师：

高效展示平移构造法的转化思想：分步演示 “平移边→构造平行四边形→证明特殊三角形→推导线段关系” 的关联链路，清晰呈现从条件到结论的完整过程，减少逻辑梳理的繁琐；
适配平行四边形教学场景：借助 “平移边构特殊四边形” 的辅助线思路，辅助引导学生梳理 “平行四边形性质→平移集中分散线段→特殊三角形性质推导关系” 的逻辑，提升课堂讲解效率。

为什么选考生网的这个模型：

“平行四边形 + 平移 + 特殊三角形” 是四边形综合题的核心考点，很多同学因 “不会通过平移集中分散线段”“特殊图形与已知条件的关联混乱” 丢分 —— 这个模型通过平移将分散的 BE、CD 与 BD 集中到同一线段（BF）上，转化为等边三角形的边长关系，推导过程直观清晰，帮助学生建立 “平行四边形中线段关系证明优先平移构特殊图形” 的解题习惯。