与圆周角、圆心角有关的辅助线典例2_动态模型演示

与圆周角、圆心角有关的辅助线典例 2 操作说明

操作指南

功能按钮：

初始化：恢复模型初始布局，重置所有展示状态；
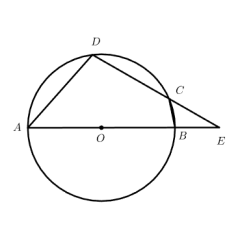
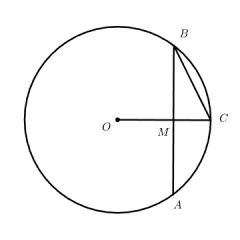
全显示：展示⊙O、直径 AB、切线 DE、弦 CE 的完整结构，清晰呈现 BF=2、EF=3 的核心条件；
上一步 / 下一步：逐步推进辅助线（连接 OE、BE）的构造过程，直观呈现 “圆周角与圆心角关联” 的辅助线逻辑；

视图与全屏：拖动图形区域可调整展示位置；点击 “全屏播放” 切换全屏模式，适配沉浸式观察；全屏下按键盘 “ESC” 键可退出。

用途说明

对学生

掌握圆周角与圆心角的辅助线方法：通过 “上一步 / 下一步” 功能，分步学习核心解题逻辑：

（1）证明∠A=2∠BCE：
连接 OE（核心辅助线，DE 是切线→OE⊥DE），由切线性质得∠OED=90°，故∠D+∠DOE=90°；
因 AB 是直径，∠ACB=90°，故∠A+∠ABC=90°；结合已知∠D=∠ABC，得∠A=∠DOE；
由 OE=OC（半径），∠DOE 是△OCE 的外角，故∠DOE=2∠BCE，因此∠A=2∠BCE。
（2）求⊙O 的半径：
连接 BE（核心辅助线），由∠BEF=∠A（第一问结论推导）、∠BFE=∠EFA，得△BEF∽△EAF；
由相似性质得EF2=BF×AF，代入 EF=3、BF=2，得9=2×AF，故AF=29；
直径AB=AF+BF=29+2=213，因此⊙O 的半径为413，解决 “圆周角与切线结合题中辅助线构造及线段计算无思路” 的问题。

对教师

高效展示圆周角与切线的综合推导过程：分步演示 “连接 OE、BE” 的辅助线构造，以及切线性质、圆周角 - 圆心角关系、相似三角形的关联链路，清晰呈现从条件到结论的完整过程，减少手动绘图与逻辑梳理的繁琐；
适配圆的综合题教学场景：借助 “全显示” 功能，直观展示直径、切线与辅助线的结构关联，辅助引导学生梳理 “切线连半径→圆周角 - 圆心角转化→相似三角形求线段” 的逻辑，提升课堂讲解效率。

为什么选考生网的这个模型

“圆周角与圆心角关联” 是圆类综合题的核心考点，很多同学因 “忽略切线连半径的辅助线”“圆周角与圆心角的转化混乱” 丢分 —— 这个模型通过分步演示辅助线构造，把抽象的 “切线→半径→角转化→相似” 逻辑变直观，条件到半径的推导链路清晰对应，帮助学生建立 “切线必连半径、角转化必找圆周角 - 圆心角关系” 的解题习惯。

成为考生网会员，不仅能无限制使用这个模型，还能解锁更多圆类辅助线典例模型，另有真题专项训练、教师在线讲题等福利，让圆类几何题从 “难下手” 变 “按步推导”，轻松拿下中考几何分数！