初中几何模型 - 8 字相似模型典例 2 操作说明
一、操作指南
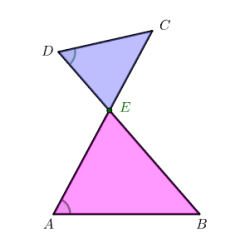
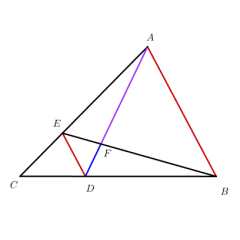
初始化布局点击 “初始化” 按钮,可将图形恢复至基础状态:呈现△ABC(AB=6)、点 D 在 AB 上、点 E 在 AC 上、DE 延长交 BC 的延长线于点 F(BF=8),重置所有元素的默认状态。
全显示构造点击 “全显示” 按钮,可一次性展示解题核心构造:标注∠A=∠F、CE=2DE 的条件,展示△ADE 与△FCE 的 8 字相似标识(AA 相似:∠A=∠F,∠AED=∠FEC),以及辅助推导的线段比例标注。
分步演示点击 “下一步” 按钮,按解题逻辑逐步呈现流程:
第一步:通过∠A=∠F(已知)、∠AED=∠FEC(对顶角相等),推导△ADE∽△FCE(AA 相似);
第二步:由 CE=2DE,得相似比 DE:CE=1:2,因此对应边 AD:FC=1:2,设 AD=x,则 FC=2x;
第三步:由∠A=∠F 推导 AB∥CF(内错角相等),进而得△ADB∽△FDC,对应边比例与已知线段(BF=8、AB=6)关联;
第四步:代入比例式建立方程,计算得 AD 的长度;点击 “上一步” 按钮,可回退至前一推导环节。
二、用途说明与应用场景(一)学生端(针对 “8 字相似 + 多组比例推导” 场景)
识别相似条件:掌握 “角相等 + 对顶角” 推导 AA 相似的方法,明确△ADE∽△FCE 的依据;
应用相似比例:通过相似三角形的对应边比例(DE:CE=1:2→AD:FC=1:2)建立线段关系;
结合平行与相似:由角相等推导直线平行,进而应用第二组 8 字相似(△ADB∽△FDC)完成线段计算。
(二)教师端(针对 “8 字相似的分层应用” 教学场景)
演示推导逻辑:通过全显示与分步按钮,展示 “找角→证相似→得比例→建方程” 的完整流程,强化 8 字相似的应用思维;
分层适配教学:基础层聚焦 “单一 8 字相似的推导”,进阶层聚焦 “平行触发的多组相似综合应用”;
提升综合能力:引导学生通过设未知数、关联多组比例,建立方程求解线段长度。
三、教学应用案例
情境导入(4 分钟)展示初始图形,提出问题:“△ABC 中,D、E 在 AB、AC 上,DE 延长交 BC 延长线于 F,已知∠A=∠F、CE=2DE,如何用 8 字相似求 AD 的长度?”
操作演示(8 分钟)
点击 “初始化”,引导识别 “∠A=∠F、CE=2DE、BF=8、AB=6” 的核心条件;
点击 “全显示”,展示△ADE 与△FCE 的相似标识,暂停提问:“这组三角形相似的依据是什么?”;
点击 “下一步”,推导相似比并设 AD=x、FC=2x,暂停提问:“∠A=∠F 能推出哪两条直线平行?”;
继续点击 “下一步”,展示 AB∥CF 触发的△ADB∽△FDC,代入已知线段建立方程,计算得 AD=2。
互动任务(3 分钟)
基础层任务:描述△ADE 与△FCE 相似的依据,及对应的边比例关系;
进阶层任务:说明 AB∥CF 的推导依据,并解释△ADB 与△FDC 的相似比例如何用于计算 AD。
总结(2 分钟)梳理核心逻辑:“本题先通过‘角相等 + 对顶角’证得△ADE∽△FCE,得到线段比例;再由角相等推导 AB∥CF,触发第二组 8 字相似,最终结合已知线段建立方程求出 AD,是多组 8 字相似综合应用的典型题型。”
 浏览量:513
浏览量:513