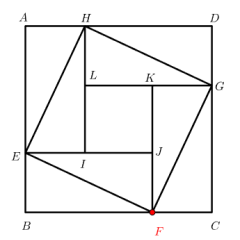
点拖动：点 F 可在小正方形边上拖动，调整位置后会同步展示直角三角形边长（x、y）的变化，可观察不同边长下大正方形、小正方形的面积关联。

功能按钮：

初始化：恢复模型初始布局，重置所有展示状态；

全显示：展示弦图完整结构（四个全等直角三角形 + 小正方形 + 大正方形），清晰呈现 x、y 与大 / 小正方形的边长关联；

上一步 / 下一步：逐步推进弦图的拼接过程，直观呈现四个直角三角形的组合逻辑；

启动 F 点 / 暂停 F 点：播放 / 暂停点 F 的动态演示，同步展示 x、y 的长度变化对图形结构的影响；

全等复位：恢复四个直角三角形的全等对齐状态，清晰标注全等边、角的对应关系；

全等演示：动态展示四个直角三角形的全等变换过程，强化 “全等” 这一核心条件的认知。

视图与全屏：拖动图形区域可调整展示位置；点击 “全屏播放” 切换全屏模式，适配沉浸式观察；全屏下按键盘 “ESC” 键可退出。

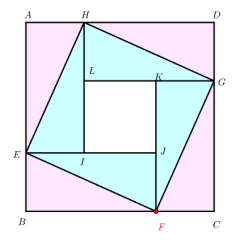
验证弦图的核心数量关系：通过 “全显示”“全等演示” 功能，可直观推导题目中的四个说法：

①大正方形边长为直角三角形斜边，故面积 x²+y²=25，正确；

②小正方形边长为较长直角边减较短直角边，故 x-y=3（小正方形面积 9，边长 3），正确；

③大正方形面积 = 4 个直角三角形面积 + 小正方形面积，即 2xy+9=25，正确；

④由 x-y=3 和 x²+y²=25，可推得 (x+y)²=34，故 x+y=√34≠7，错误；

借助模型的结构展示，解决 “数量关系与图形结构衔接混乱” 的问题。

强化勾股定理的应用逻辑：拖动点 F 改变 x、y 的长度，同步观察大 / 小正方形的面积变化，深化 “边长→面积→勾股定理” 的关联认知，适配中考弦图类勾股定理题型。

高效拆解弦图的数量关系：通过 “上下步”“全等演示” 功能，分步展示图形拼接与全等关系，清晰推导 x²+y²、x-y 等数量关系的来源，减少手动推导的繁琐；

适配多教学场景：借助 “启动 F 点”“全等复位” 功能，可按需展示动态变化或静态全等状态，适配 “图形拼接”“数量关系推导” 等不同教学重点。