初中几何模型 - 赵爽弦图典例 02 操作说明

操作指南

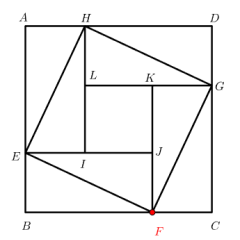
1. 点拖动：点 F 可在 BC 边上拖动，调整位置后会同步改变直角三角形的边长，可观察不同边长下三个正方形（ABCD、EFGH、IJKL）的面积变化。

2. 功能按钮：

• 初始化：恢复模型初始布局，重置所有展示状态；

• 全显示：展示弦图完整结构及三个正方形的面积关联元素；

• 上一步 / 下一步：逐步推进弦图的拼接过程，清晰呈现八个全等直角三角形的组合逻辑；

• 启动动点 / 暂停动点：播放 / 暂停弦图的动态拼接过程，直观展示正方形的形成逻辑；

• 全等边：标注所有相等的线段（如直角三角形的直角边、斜边），辅助面积关系的推导；

• 全高示：显示相关图形的高，清晰对应面积计算的基底。

3. 视图与全屏：拖动图形区域可调整展示位置；点击 “全屏播放” 切换全屏模式，适配沉浸式观察；全屏下按键盘 “ESC” 键可退出。

用途说明

1. 攻克弦图面积关联难点：通过模型直观理解三个正方形的面积关系 ——S₁（ABCD）对应大正方形面积，S₃（IJKL）对应小正方形面积，S₂（EFGH）对应中间正方形面积；结合八个全等直角三角形的拼接逻辑，可推导得 S₁+S₃=2S₂（因 S₁=S₂+4× 直角三角形面积，S₃=S₂-4× 直角三角形面积），进而由 S₁+S₂+S₃=24 推出 3S₂=24，得 S₂=8，解决弦图面积题的推导混乱问题。

2. 强化勾股定理与面积的关联：拖动点 F 改变直角三角形边长，同步观察正方形面积与直角三角形边长的对应关系，深化 “勾股定理→边长→面积” 的逻辑链，适配中考弦图类勾股定理题型。

1. 高效展示面积推导过程：通过 “上下步”“启动动点” 功能，分步或动态演示八个全等直角三角形的拼接过程，清晰呈现 S₁、S₂、S₃的面积关联逻辑，减少手动绘图与推导的繁琐。

2. 适配多例题讲解：可调的点 F 位置能匹配不同面积条件的例题，直观展示面积关系的推导，提升课堂讲解的针对性与效率。

为什么选考生网的这个模型