1. 初始化：点击后，图形（⊙O、圆外点 P、切线 PA/PB 及相关线段）将恢复初始布局，确保模型演示的起点一致，便于重新探究或课堂演示。
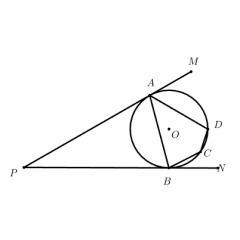
2. 全显示：一键呈现模型的核心条件（点 P 为⊙O 外一点，PA、PB 是⊙O 的切线，切点为 A、B）及对应结论（△OAP≅△OBP、∠AOB+∠APB=180∘、OP 平分∠AOB与∠APB、OP 垂直平分 AB），快速建立模型的直观认知。
3. 上一步 / 下一步：
   • 点击 “下一步”：分步展示操作（先观察点 P 在圆外的位置，明确 PA、PB 与⊙O 的切线关系；再关联△OAP与△OBP的边、角特征，推导二者的全等关系；接着分析∠AOB与∠APB的角度和关系；然后观察 OP 与∠AOB、∠APB的位置关联，验证 OP 的角平分性质；最后聚焦 OP 与 AB 的位置关系，演示 OP 垂直平分 AB 的特征），将 “切线关系观察→三角形全等推导→角度和验证→角平分性质演示→垂直平分特征展示” 的模型探究过程拆解为操作步骤，适配自主学习节奏。
   • 点击 “上一步”：回退至前一操作画面，便于回看细节、核对模型探究流程。
4. 窗口内容拖动：拖动图形区域，调整显示位置，清晰聚焦 “切线 PA/PB 的特征”“△OAP与△OBP的全等关联”“角度和的推导细节”“OP 的角平分及垂直平分性质” 等核心内容。
5. 全屏显示：点击后界面视觉更清晰，模型的条件、图形与结论演示流程同步呈现，适配教室大屏演示或个人专注学习的场景。

核心用途

• 对学生：通过分步交互操作，直观理解双切线模型的核心条件与结论逻辑，掌握 “切线特征观察→全等三角形推导→角度与线段性质验证” 的操作流程，建立双切线几何模型的认知框架。
• 对老师：借助交互步骤快速展示模型的探究流程，节省手绘、讲解时间；分步操作适配分层教学 —— 基础学生可跟随步骤掌握模型的核心性质，进阶学生能探究模型的拓展应用场景，提升课堂教学效率。