一线三等角相似典例 1（等边三角形背景下的一线三等角模型）操作说明

一、操作指南（针对 “等边三角形 + 60° 角构造的一线三等角” 模型）

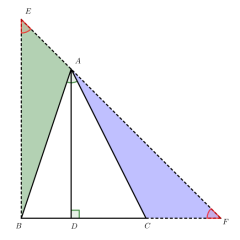
1. 初始化布局点击右上角循环箭头按钮，恢复本模型初始状态：包含边长为 7 的等边△ABC、点D（BC边）、M（AB边）、N（AC边）的基础位置，同时清除解析构造元素、重置参数滑块。

2. 解析构造元素的显隐勾选 “解析” 复选框，展示本模型的核心解题构造：关联∠MDN=60∘的辅助线（适配等边三角形的 60° 角特征）、相似三角形的角对应标注；取消勾选则隐藏构造元素，仅保留等边三角形及点的基础位置关系。

3. 参数滑块调整拖动 “b” 对应的滑块，可调整模型的关联参数，观察等边三角形内一线三等角模型的形态变化（适配点M、N的不同位置布局）。

4. 全屏展示与退出点击界面的全屏按钮，将本模型的等边三角形图形、构造元素切换至全屏模式，优化构造细节的展示清晰度；在全屏模式下，按下键盘 “ESC” 键即可恢复原界面布局。

二、用途说明与应用场景

（1）学生端（针对 “等边三角形综合题 + 一线三等角相似” 场景）

1. 梳理等边三角形与一线三等角的关联：通过 “解析” 的显隐，理清等边三角形的 60° 角特征与∠MDN=60∘构造的一线三等角之间的逻辑关系；

2. 掌握辅助线技巧：借助解析中的构造元素，明确等边三角形背景下一线三等角模型的辅助线添加方向（关联等边三角形的内角）；

3. 推导相似关系：结合解析标注，理解等边三角形内一线三等角对应的相似三角形判定逻辑，建立 “等边三角形边长→相似比例→目标线段长度” 的解题链条。

（2）教师端（针对 “八年级等边三角形综合课、九年级一线三等角相似课” 场景）

1. 分层展示构造逻辑：隐藏 “解析” 呈现基础图形，引导学生自主思考 60° 角的构造方向；勾选 “解析” 展示完整构造，辅助学生梳理逻辑；

2. 适配不同认知层次：基础层聚焦 “解析中的辅助线与等边三角形内角的关联”，进阶层聚焦 “相似三角形的判定与边长比例关系”。

三、教学应用案例（适配本模型的课堂流程）

1. 情境导入（4 分钟）展示取消 “解析” 后的基础图形，提问：“等边△ABC中，∠MDN=60∘时，如何利用等边三角形的 60° 角构造相似模型求BM的长？”

2. 操作演示（7 分钟）

• 保持 “解析” 未勾选，引导学生识别等边三角形的基础元素（边长、60° 内角）；

• 勾选 “解析”，展示构造元素，暂停提问：“解析中的辅助线是如何关联等边三角形的 60° 角与∠MDN=60∘的？”

1. 互动任务（3 分钟）

• 基础层：描述解析中的辅助线与等边三角形边（AB、AC）的位置关系；

• 进阶层：说明解析中标注的相似三角形，依据哪些条件判定相似。

1. 总结（2 分钟）梳理：“在等边三角形背景下，可借助其 60° 内角特征，结合∠MDN=60∘构造一线三等角模型，通过相似比例推导目标线段长度”