考生网初中几何模型 - 十字架模型典例 1
一、操作指南(适配考生网交互式几何学习场景)
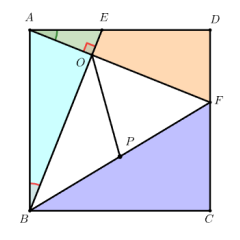
- 初始化点击 “初始化” 按钮后,包含 Rt△ACB(∠ACB=90°、AC=4、BC=3)、点 D(AC 的中点)、线段 BD、线段 CE(CE⊥BD,交 AB 于 E、交 BD 于 F)的图形会恢复至典例初始布局,确保探究起点一致,适配课堂演示与自主学习流程。
- 全显示点击 “全显示” 按钮后,会一次性呈现该典例的核心逻辑 ——“直角三角形性质关联→CE 与 BD 的垂直关系推导→相似三角形构造→线段 CE 的长度推导” 的完整链路,将 “直角三角形十字架模型 + 垂直 + 线段长度” 的复合几何关系转化为可视化步骤,降低抽象题的理解难度。
- 上一步 / 下一步
点击 “下一步”:逐步呈现 “直角三角形边与角的性质梳理→BD 的构造与 CE 的垂直关系验证→相似三角形的条件推导→线段 CE 的长度关联” 的过程,拆分中考十字架模型题型的分析步骤,辅助学生梳理图形逻辑;
点击 “上一步”:回退至前一画面,便于学生自查思路偏差、教师课堂复盘细节步骤。
- 点拖动操作拖动点 E(AB 线段区域),平台会同步调整 CE 的位置及 F 点在 BD 上的分布,直观呈现 “点 E 位置变化与 CE 长度” 的联动规律,支持学生自主探索题型逻辑。
- 窗口内容拖动调整拖动图形区域内的内容(如 Rt△ACB 的布局、线段 CE 与 BD 的相对位置),可自主调整显示位置,避开界面遮挡,适配个人观看习惯,更清晰聚焦直角三角形、垂直线段、相似三角形等关键几何元素的关联。
- 全屏播放与退出操作
点击界面中图形区域的 “全屏播放” 按钮:可将几何图形与操作界面切换至全屏模式,优化视觉布局,清晰呈现 “动点运动 - 垂直关联 - 线段推导” 的逻辑链,适配教室大屏演示、学生沉浸式学习的场景;
退出全屏:在全屏模式下,按下键盘 “ESC” 键,即可快速退出全屏状态,恢复原界面布局。
二、用途说明(含分层教学适配)
(1)对学生
精准突破中考综合考点
聚焦 “直角三角形十字架模型 + 垂直 + 线段长度” 这一中考几何综合难点,通过交互操作自主梳理 “直角三角形性质 - 垂直关系 - 相似三角形” 的解题逻辑,攻克几何综合题的丢分点。
学习更直观高效
借助动态演示与线段长度联动功能,摆脱被动记忆,将 “直角三角形内复合几何条件的线段长度问题” 抽象原理转化为可视可操作的过程,提升理解深度与解题效率。
构建系统化知识体系
结合考生网 “直角三角形几何系列”“十字架模型系列” 模型,联动训练同类综合题,构建覆盖中考几何核心题型的知识框架。
(2)对教师
轻松演示复杂题型
无需手绘直角三角形、垂直线段、相似三角形等图形,通过 “全显示 + 下一步” 功能 5 分钟即可讲透 “直角三角形十字架模型 + 垂直” 的图形逻辑,大幅节省课堂板书与演示时间。
分层教学适配全层次学生
基础层学生:通过 “全显示” 聚焦相似三角形与线段的核心结论,配套 “标记垂直线段位置” 的任务,帮助后进生掌握题型的图形基础;
进阶层学生:引导自主拖动动点,观察不同位置下的线段长度变化,总结 “直角三角形十字架模型 + 垂直” 的解题共性;
拔高层学生:布置 “调整直角三角形边长的线段长度变式题”,借助模型拓展解题思路;
丰富综合课教案内容
预设的交互步骤可直接整合至几何综合课教案,让综合题课从 “枯燥讲题” 转变为 “互动探究”,提升学生的参与度与理解效率。
三、教学应用案例与实施策略
(1)课堂教学案例:八年级 “直角三角形十字架模型 + 垂直” 探究课(20 分钟片段)
情境导入
展示 “直角三角形内由垂直线段构造的线段长度问题” 的几何情境,提问 “如何推导 CE 的长度关联?”,引出本模型;
模型操作
点击 “下一步” 按钮,逐步呈现直角三角形性质、垂直关系的关联过程,引导学生识别相似三角形与线段的逻辑;
拖动图形内容调整显示位置,清晰展示 “直角三角形 - 动点 - 垂直线段” 的关联关系;
分层任务
基础层:跟着操作标记相似三角形的对应边,梳理 CE 长度的核心推导步骤;
进阶层:自主拖动点 E,记录不同位置下的 CE 长度变化;
拔高层:尝试调整直角三角形的边长,设计 “新边长下的 CE 长度” 拓展问题;
总结反馈
各层次学生分享结果,借助 “全显示” 功能梳理 “直角三角形十字架模型 + 垂直” 的核心图形逻辑,强化认知。
 浏览量:1460
浏览量:1460