构造“半角”模型典例_动态模型演示

考生网初中几何模型 - 构造 “半角” 模型典例（三角形场景）

操作功能说明

・初始化：点击后图形恢复题干初始布局（△ABC、点 D/E 等元素），条件与题目要求完全匹配。

・全显示：点击后呈现该题完整解题逻辑，直接展示 “半角条件下 DE 长度” 的推导链路。

・分步操作：点击 “上一步 / 下一步”，可推进或回退解题步骤，逐步展示等边三角形性质、角的关系等核心推导环节。

・视窗调整：可拖动图形区域，自由调整显示位置，聚焦△ABC 结构、半角关联的角与线段关系细节。

・全屏显示：点击界面右下角的全屏按钮，可切换至全屏模式展示模型；按 ESC 键可退出全屏模式。

核心用途说明

对学生
・攻克解题难点：聚焦 “△ABC（∠BAC=120°）+ 等边△ADE” 类题目，通过操作梳理 “利用等边三角形性质 + 半角关联角的等量关系→证三角形相似→推导线段长度” 的逻辑，避免思路混乱。
・提升效率：借助 “分步操作 + 全显结论”，直观跟踪解题流程，把抽象的三角形半角场景下的线段长度问题转化为可落地的推导步骤。
对教师
・简化教学：无需手绘复杂的角与线段标注，通过 “初始化 + 全显示”，5 分钟讲清三角形中半角关联场景下线段长度的求解方法，节省板书时间。
・适配分层：基础弱的学生可直接查看结论；进阶学生可分步操作，自主推导等边三角形性质、相似三角形判定等细节。

教学应用指南

・课堂导入：初始化图形后提问 “△ABC 中∠BAC=120°，D、E 在 BC 上且△ADE 是等边三角形，已知 BD=3、CE=1，怎么求 DE 的长？”，切入核心思路。

・难点突破：

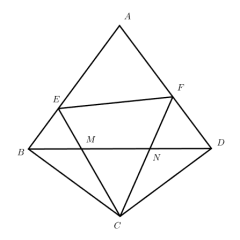
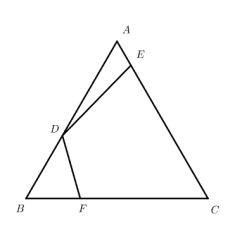
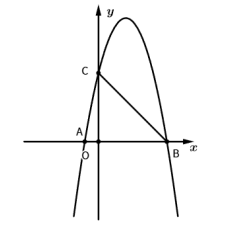
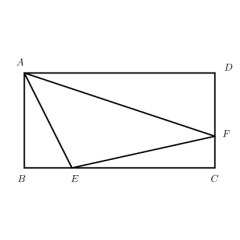
・分析基础性质：由 AD=AE=DE，得△ADE 是等边三角形，故∠ADE=∠AED=60°，进而∠ADB=∠AEC=180°-60°=120°。
・推导角的等量关系：因∠BAC=120°，故∠BAD+∠CAE=120°-∠DAE=60°；又∠ADB=120°，故∠B+∠BAD=60°，因此∠B=∠CAE。
・证相似求长度：由∠B=∠CAE、∠ADB=∠AEC，证得△ABD∽△CAE；设 DE=x（则 AD=AE=x），由相似比得 3/x = x/1，解得 x=√3，故 DE 的长为√3。
・课后巩固：按照 “初始化→下一步→全显示” 的操作流程，总结 “三角形 + 半角关联 + 等边三角形，优先利用角的等量关系证相似，再通过相似比求线段长度” 的规律。