初中几何模型 - 共边共角型相似 (射影定理) 2 操作说明
一、操作指南
初始化布局
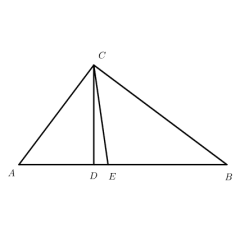
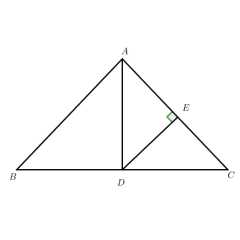
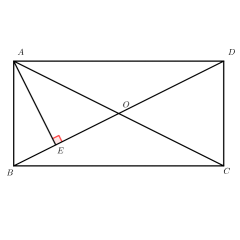
点击 “初始化” 按钮,可将模型恢复至初始状态:呈现 Rt△ABC(CD⊥AB)的基础图形,重置所有滑块、元素的状态,回归默认的图形与条件展示。
相似与模型演变演示
拖动 “△CDB~△ADC” 滑块:展示该组三角形的共边共角型相似对应关系,同步关联射影定理的比例中项结论;
拖动 “△ADE 翻折 - 旋转”“△BDC 翻折 - 旋转” 滑块:分别演示对应三角形经翻折、旋转后,逐步形成当前 “直角三角形 + 高”(射影定理)共边共角型相似模型的动态过程。
动点操作
拖动点 C(说明中标注可拖动):改变其空间位置,观察 Rt△ABC 与 CD 的形态变化,同时验证 “△ACD~△ABC”“△BCD~△BAC”“△ACD~△CBD” 的相似关系及射影定理结论的稳定性。
二、用途说明与应用场景
学生端(针对 “共边共角型相似与射影定理的融合认知” 场景)
明确模型本质:掌握该模型是共边共角型相似在直角三角形中的特殊应用(即射影定理),核心条件为 “Rt△ABC+CD⊥AB”;
掌握核心结论:熟练识别 Rt△ABC 中 CD⊥AB 时的三组共边共角型相似三角形,以及对应的射影定理比例中项(AC2=AD⋅AB、BC2=BD⋅AB、CD2=AD⋅BD);
关联相似与射影:理解射影定理的结论是由共边共角型相似三角形的比例关系推导而来。
教师端(针对 “共边共角型相似与射影定理的关联教学” 场景)
直观演示关联:通过滑块展示 “普通共边共角型相似→射影定理模型” 的演变,帮助学生建立相似模型与射影定理的联系;
分层适配教学:基础层聚焦 “三组相似三角形的识别”,进阶层聚焦 “射影定理比例中项的推导”;
完善体系认知:将射影定理纳入共边共角型相似的模型体系,强化几何知识的系统性。
三、教学应用案例(适配共边共角型相似与射影定理关联课流程)
情境导入(4 分钟)展示初始化后的模型,提出问题:“Rt△ABC 中 CD⊥AB,这一图形属于共边共角型相似吗?它能推导出具象的结论吗?”
操作演示(8 分钟)
点击 “初始化”,引导学生识别 “Rt△ABC、CD⊥AB” 的核心条件;
拖动 “△CDB~△ADC” 滑块,展示相似关系,暂停提问:“这组相似对应的比例关系是什么?”;
拖动翻折 - 旋转滑块,演示模型演变,暂停提问:“射影定理模型是由普通共边共角型相似经什么变换得到的?”;
拖动点 C,验证结论稳定性,提问:“点 C 移动后,射影定理的比例中项关系还成立吗?”
互动任务(3 分钟)
基础层任务:描述 Rt△ABC 中 CD⊥AB 时的三组相似三角形;
进阶层任务:推导射影定理的任意一条比例中项结论,并说明其与共边共角型相似的关联。
总结(2 分钟)梳理核心逻辑:“本模型是共边共角型相似在直角三角形中的特殊应用,即射影定理,其三组相似三角形对应三条比例中项结论,是共边共角型相似与直角三角形性质融合的典型几何模型。”
 浏览量:1663
浏览量:1663