初中几何模型 - 相似模型 (共边共角等腰) 操作说明
一、操作指南
初始化布局
点击右上角的循环箭头按钮,可将模型恢复至初始状态:重置图①、图②的显示状态,复位所有滑块与复选框,回归默认的图形与条件展示。
图形切换显示
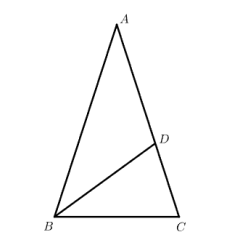
勾选 “图①等腰三角形” 复选框:展示图①对应的图形(△ABC,∠ABC=∠C=72°)及相关条件、结论;
勾选 “图②等腰三角形” 复选框:展示图②对应的图形(△ABC,∠B=∠C=36°)及相关条件、结论;
可单独勾选某一复选框展示对应图形,也可同时勾选展示两种模型的对比。
相似关系演示
拖动 “△BCD∽△ABC” 滑块:动态演示图①中△BCD 与△ABC 的相似对应关系,同步呈现 “BC²=CD・AC” 的比例中项关系,以及 “CD=(√5-1)/2 AD” 的黄金分割比例;
拖动 “△DAB∽△ABC” 滑块:动态演示图②中△DAB 与△ABC 的相似对应关系,同步呈现 “AB²=BD・BC” 的比例中项关系,以及 “BD=(√5-1)/2 CD” 的黄金分割比例。
二、用途说明与应用场景
学生端(针对 “共边共角等腰相似模型的认知与应用” 场景)
理解模型核心条件:明确 “共边共角 + 等腰” 是该相似模型的关键(如图①共边 BC、共角∠C,图②共边 AB、共角∠B);
掌握比例关系:熟练应用 “公共边的平方 = 邻边・第三边” 的比例中项结论,同时认知黄金分割比例在该模型中的体现;
区分模型类型:识别 “72° 角”“36° 角” 两种等腰三角形对应的相似关系差异。
教师端(针对 “共边共角等腰相似的分类教学” 场景)
高效演示模型对比:通过复选框切换图①、图②,直观呈现两种共边共角等腰相似的差异与共性;
分层适配教学:基础层聚焦 “相似关系的判定与比例中项结论”,进阶层聚焦 “黄金分割比例的推导与应用”;
关联拓展知识:将该模型与黄金分割、等腰三角形性质串联,强化知识点的融合应用。
三、教学应用案例(适配共边共角等腰相似模型课流程)
情境导入(4 分钟)展示初始化后的模型,提出问题:“等腰三角形中,当存在共边共角的条件时,会形成怎样的相似关系?不同角度的等腰三角形对应的相似结论有何差异?”
操作演示(8 分钟)
点击循环箭头初始化,引导学生识别模型的 “共边共角 + 等腰” 核心特征;
勾选 “图①等腰三角形” 复选框,拖动对应滑块,暂停提问:“图①中△BCD 与△ABC 的相似判定依据是什么?比例中项关系如何推导?”;
勾选 “图②等腰三角形” 复选框,拖动对应滑块,暂停提问:“图②的相似关系与图①有何不同?黄金分割比例在其中如何体现?”。
互动任务(3 分钟)
基础层任务:分别描述图①、图②的相似三角形及对应的比例中项关系;
进阶层任务:推导图①中 “CD=(√5-1)/2 AD” 的黄金分割比例,说明推导依据。
总结(2 分钟)梳理核心逻辑:“共边共角等腰相似模型是等腰三角形与相似三角形的融合应用,核心是‘共边共角’触发相似,结论包含比例中项与黄金分割;72°、36° 角的等腰三角形是该模型的典型载体,也是中考几何中黄金分割类题型的常见背景。”
 浏览量:1662
浏览量:1662