初中几何模型 - 勾股定理探究 1
一、操作指南(适配考生网交互式几何学习场景)
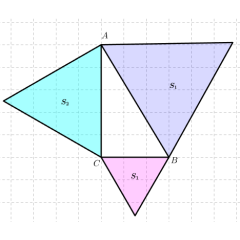
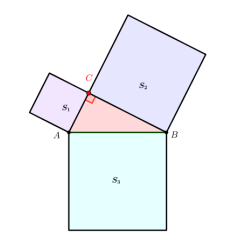
初始化布局点击界面右上角的循环箭头按钮,恢复初始布局:即 B 点水平向右 3 格、A 点垂直向上 3 格对应的 Rt△ABC,以及以其三边为边长所作的正方形(标识为 S₁、S₂、S₃),同时下方面积表格恢复初始数值(S₁=9、S₂=9、S₃=18)。
点位置调整
拖动 “B 向右 3” 对应的控制点,调整 B 点的水平位置,改变 Rt△ABC 的水平直角边长度;
拖动 “A 向上 3” 对应的控制点,调整 A 点的垂直位置,改变 Rt△ABC 的垂直直角边长度;调整过程中,以三边为边长的正方形(S₁、S₂、S₃)的形态会随 Rt△ABC 的边长同步变化。
面积关系查看界面下方的表格会实时更新 S₁、S₂的面积,以及 S₁+S₂、S₃的数值,直观呈现 “斜边对应正方形面积(S₃)与两直角边对应正方形面积和(S₁+S₂)” 的等价关系。
全屏展示与退出点击界面的全屏按钮,可将网格、图形及面积表格切换至全屏模式,优化展示效果;在全屏模式下,按下键盘 “ESC” 键即可恢复原界面布局。
二、用途说明(含分层教学适配)
(1)对学生
掌握勾股定理的核心面积应用通过调整 A、B 点的位置,观察不同边长的 Rt△ABC 对应的 S₁、S₂、S₃面积变化,明确 “直角三角形斜边对应的正方形面积,等于两直角边对应的正方形面积和”,建立勾股定理的核心面积认知。
强化动态验证的逻辑认知借助点位置调整与面积表格的实时更新,动态验证勾股定理在正方形面积场景中的普适性,深化 “边长平方关系→正方形面积关系” 的关联理解。
构建网格下的几何测量思维结合网格背景,形成 “通过坐标 / 格数确定边长,进而推导正方形面积” 的几何测量逻辑,提升网格场景下的基础几何分析能力。
(2)对教师
高效展示多案例验证过程无需手动绘制不同边长的 Rt△ABC 及对应正方形,通过拖动控制点快速切换案例,同步查看面积关系,节省课堂中多案例验证的时间。
分层教学适配全层次学生
基础层学生:固定 A、B 点位置,观察初始布局下的面积表格,明确勾股定理对应的正方形面积关系;
进阶层学生:自主调整 A、B 点位置,记录多组边长对应的面积数据,总结 “斜边正方形面积 = 直角边正方形面积和” 的核心规律。
丰富课堂互动形式以 “点拖动 + 实时面积更新” 替代静态板书验证,让勾股定理的探究更具互动性与直观性,提升学生的参与度。
三、教学应用案例与实施策略
(1)课堂教学案例:八年级 “勾股定理的正方形面积验证” 操作课(20 分钟片段)
情境导入展示初始布局的图形与面积表格,提问 “直角三角形三边对应的正方形,面积有怎样的数量关系?”,引出本探究的操作演示;
模型操作
点击重置按钮,恢复初始布局,引导学生观察表格中 “S₁+S₂”(9+9)与 “S₃”(18)的数值等价性;
拖动 “B 向右 3” 的控制点,调整 B 点位置,让学生观察正方形形态变化,同步查看表格中面积数值的更新;
拖动 “A 向上 3” 的控制点,调整 A 点位置,重复观察图形与面积的关联变化;
点击全屏按钮,在大屏清晰展示网格、图形与表格;
分层任务
基础层:记录初始布局下的面积数据,描述 “S₁、S₂、S₃” 的面积关系;
进阶层:自主调整 A、B 点位置 2 次,记录对应面积数据,说明每次调整后 “斜边正方形面积与直角边正方形面积和” 的关系;
总结反馈引导学生结合操作内容,总结 “勾股定理探究 1 的操作要点(核心:直角三角形三边对应的正方形,面积符合‘斜边正方形面积 = 直角边正方形面积和’;操作:通过点拖动验证多案例)”,强化对勾股定理核心面积关系的认知。

 浏览量:524
浏览量:524