初中几何模型 - 勾股树模型 - 月牙定理(希波克拉底)
一、操作指南(适配考生网交互式几何学习场景)
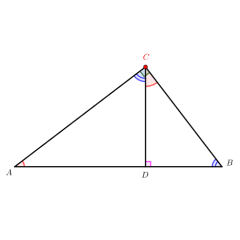
初始化点击 “初始化” 按钮后,包含 Rt△ABC(∠C=90°)、以 AB/AC/BC 为直径的半圆(形成月牙 S₁、S₂)的图形会恢复至典例初始布局,重置所有展示状态,确保探究起点一致。
全显示点击 “全显示” 按钮后,会一次性呈现 “Rt△ABC(∠C=90°)的标注→以 AB、AC、BC 为直径的半圆的图形标注→月牙 S₁、S₂的面积区域标注” 的完整元素,明确月牙定理的核心图形结构。
步骤切换(上一步 / 下一步)点击 “下一步” 按钮,可逐步展示月牙定理模型的构建流程(点击 “上一步” 可回退):
操作步骤 1:展示 “绘制 Rt△ABC(∠C=90°)” 的基础图形;
操作步骤 2:展示 “以 AC、BC 为直径作半圆” 的图形添加效果;
操作步骤 3:展示 “以 AB 为直径作半圆” 的图形添加效果(形成月牙区域);
操作步骤 4:展示 “月牙 S₁、S₂的区域标注”。
C 点动画与暂停
点击 “C 点动画” 按钮,展示点 C 在保持∠C=90° 的前提下运动的过程,观察不同直角三角形布局下月牙模型的变化;
点击 “暂停 C 点” 按钮,可停止点 C 的动画,固定当前图形布局。
数据验证勾选 “数据验证” 选项,可展示 “月牙 S₁、S₂的面积和与 Rt△ABC 的面积” 的数量关系数据,直观验证希波克拉底月牙定理的结论。
C 点拖动调整拖动点 C(保持∠C=90°),可自主调整 Rt△ABC 的形状,观察月牙定理在不同直角三角形下的普适性。
全屏播放与退出点击界面中图形区域的 “全屏播放” 按钮:可将模型与操作界面切换至全屏模式,优化展示效果;退出全屏:在全屏模式下,按下键盘 “ESC” 键,即可恢复原界面布局。
二、用途说明(含分层教学适配)
(1)对学生
掌握月牙定理的图形操作策略通过分步展示与动画操作,明确 “以直角三角形三边为直径作半圆→形成月牙区域” 的图形构建策略,攻克月牙定理的图形识别与构造难点。
强化勾股定理的拓展应用能力借助数据验证与 C 点拖动操作,理解 “月牙面积和与直角三角形面积的等价关系”,掌握勾股定理在面积(半圆、月牙)场景中的拓展应用。
构建勾股树模型的操作体系结合考生网 “初中几何模型” 系列内容,联动理解 “直角三角形→半圆→月牙” 的勾股树模型特征,形成以图形构造为核心的月牙定理分析框架。
(2)对教师
高效展示月牙定理的动态构建逻辑无需手动分步绘制图形,通过 “步骤切换 + C 点动画” 快速呈现模型的构建与变化过程,节省课堂中定理演示的时间。
分层教学适配全层次学生
基础层学生:通过步骤展示,配套 “标记 Rt△ABC 与月牙区域” 的任务,掌握基础图形操作步骤;
进阶层学生:结合数据验证与 C 点拖动,梳理 “勾股定理→半圆面积关系→月牙面积与三角形面积等价” 的逻辑链条,总结月牙定理的应用规律。
丰富课堂互动形式以 “动画演示 + 数据验证 + 点拖动” 替代传统板书讲解,让月牙定理的探究更具动态性与直观性,提升学生课堂参与度。
三、教学应用案例与实施策略
(1)课堂教学案例:八年级 “勾股树模型 - 月牙定理” 操作课(20 分钟片段)
情境导入展示初始布局的月牙定理模型,提问 “直角三角形三边对应的半圆围成的月牙区域,其面积与三角形面积有怎样的关系?”,引出本模型的操作演示;
模型操作
点击 “初始化”,恢复模型初始布局;
点击 “全显示”,完整呈现 Rt△、半圆、月牙的所有元素;
点击 “下一步”,逐步展示模型构建流程,引导学生识别每一步的图形元素;
点击 “C 点动画”,展示 C 点运动时模型的变化;
勾选 “数据验证”,展示面积关系数据;
拖动 C 点调整位置,观察定理的普适性;
点击全屏按钮,在大屏展示完整操作流程;
分层任务
基础层:在展示界面中标记 Rt△ABC 与月牙 S₁、S₂的区域,明确模型的基础图形元素;
进阶层:结合数据验证结果,自主描述月牙面积与 Rt△ABC 面积的关系,梳理其与勾股定理的关联逻辑;
总结反馈引导学生结合操作内容,总结 “月牙定理的操作要点(核心:直角三角形 + 三边半圆→月牙面积等价于三角形面积;操作:通过动画与拖动验证普适性)”,强化对勾股树模型中月牙定理的认知。
 浏览量:1304
浏览量:1304